The Brown Center released a report today called “The Algebra Imperative.” The report shows that current national and international math assessments do not adequately measure how well American students are learning algebra. In this chalkboard post, I elaborate upon a point made in the report: that taking and successfully completing an Algebra II course, which once certified high school students’ mastery of advanced topics in algebra and solid preparation for college-level mathematics, no longer means what it once did. The credentialing integrity of Algebra II has weakened.
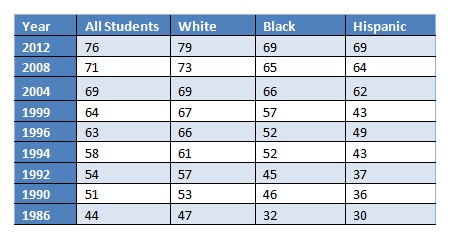
The declining significance of successfully completing Algebra II highlights a dilemma. Pushing students to take more advanced coursework has been a mainstay of American school reform for several decades. That prescription has worked in boosting enrollments. In 1986, less than half of all 17 year-olds (44%) had completed Algebra II, and for Black and Hispanic students, the rate was less than a third. Completing Algebra II is now commonplace. In 2012, about three-fourths of students completed Algebra II, and the race/ethnicity gaps associated with taking the course have narrowed significantly. (All NAEP data below are from the NAEP data explorer.)
Table 1. Percentage of 17 Year-Olds who Completed Second Year Algebra (1986-2012)
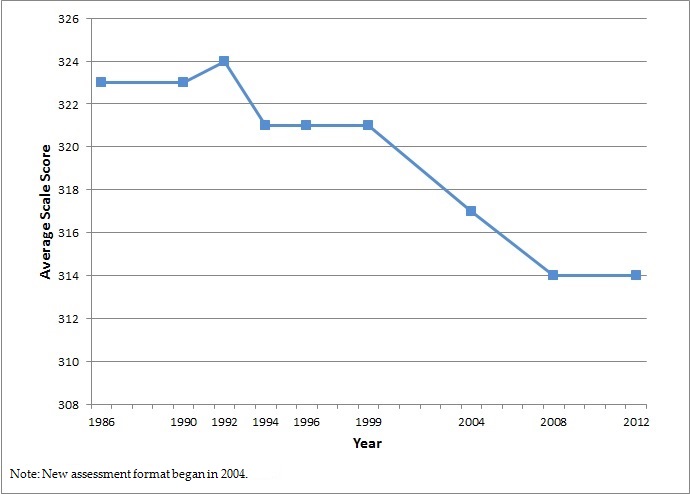
Getting more students to take higher level math courses may be a hollow victory. It has not coincided with students learning more math. Figure I shows the average NAEP scores for Algebra II completers (in the following discussion, “completers” include students enrolled in the course when they took NAEP). As enrollments boomed, test scores went down. Caution must be exercised in infering causality. We cannot be certain of a causal connection between rising enrollments and falling scores, but it is certainly plausible—even likely–that enrollment gains have been achieved by drawing in students who are not prepared to take the course. Research does not indicate a decline in the quality of Algebra II teachers or Algebra II textbooks or some other deterioration in course components from 1986-2012 that can explain the decline in NAEP scores.
Figure 1. NAEP Math, 17 Year-Olds who have Completed Second Year Algebra (1986-2012)
A Pipeline Problem
Previous research has documented serious problems in the earliest stages of the advanced math pipeline, in which students traditionally progressed from Algebra I to a final course (Pre-Calculus or Calculus) over four or five years. More and more unprepared students are being pushed into advanced math in middle school. In 2008, I published a study analyzing eighth grade NAEP data. The data were from 2005, and even then a large percentage of low achievers (about 29% of those performing at the 10th percentile or lower in math) were enrolled in advanced math courses. I called these students “Misplaced Math Students” because they did not function at a level commensurate with their math courses. They functioned at about the second to third grade level. They were students who had trouble answering NAEP items involving fractions, decimals, and percentages, concepts that should have been learned several years earlier, and yet they were enrolled as middle schoolers in courses that until recently were considered high school courses.
Several subsequent studies have raised questions about policies that make low performing students take Algebra I in 8th grade.[i] A study out of California found that marginal math students who spent one more year before tackling Algebra I were 69% more likely to pass the algebra end of course exam in 9th grade than ninth grade peers who were taking the course for the second time after failing the algebra test in 8th grade. The researchers referred to a “leaky pipeline” put under increased pressure by California’s aggressive placement of low achieving 8th graders in algebra. The policy succeeded in boosting middle school enrollments in Algebra I, but a large number of students quit taking math just as soon as they could in high school. Even low achievers who matriculate into higher level math courses may not benefit. A study of Charlotte-Mecklenburg students by Clotfelter, Ladd, and Vigdor found that low achievers who took 8th grade algebra experienced negative long term effects, including lower pass rates in Geometry and Algebra II.
Consequences
The misplaced students are not the only ones who pay a price. Recent studies suggest that a systematic erosion of the legitimacy of advanced courses is taking place. By that I mean: students are taking advanced, college-prep courses, passing them with good grades, and yet do not know the advanced subject matter signified by the titles of the courses they have taken. Courses have lost their credentialing power. An National Center for Education Statistics (NCES) study of high school transcripts analyzed the textbooks students used in high school Algebra I, Geometry, and Integrated Math courses. NCES conducted the study to solve a riddle.
The 2005 National Assessment of Educational Progress (NAEP) High School Transcript Study (HSTS) found that high school graduates in 2005 earned more mathematics credits, took higher level mathematics courses, and obtained higher grades in mathematics courses than in 1990. The report also noted that these improvements in students’ academic records were not reflected in twelfth-grade NAEP mathematics and science scores. Why are improvements in student coursetaking not reflected in academic performance, such as higher NAEP scores?[ii]
The researchers found that course titles often don’t mean what they say. NCES Commissioner Jack Buckley summarized the study’s main finding in an interview with Education Week, “We found that there is very little truth in labeling for high school Algebra I and Geometry courses.”[iii]
As unprepared students flow through a series of counterfeit courses, the entire curricular system is corrupted. Algebra II teachers are expected to teach mathematics to students who passed Algebra I with good grades but who, in reality, have not mastered elementary grade concepts that are fundamental to understanding algebra. Parents get false signals about how well their sons and daughters are prepared for college. Schools misallocate resources dedicated to remedial programs by assuming that students know material that they, in fact, do not know.
In the end, the transition to college unmasks the charade. In California, the California State University System draws students from the top one-third of graduating seniors. In 2012, about 30% of entering freshmen taking the Entry Level Math test failed the exam and were placed in remedial math classes, despite earning a mean GPA of 3.15 in college prep high school programs. That doesn’t make sense. Good grades in tough courses, yet remediation was needed.[iv]
The problem is not confined to California. Nor is it limited to mathematics. A report from the National Center for Public Policy and Higher Education (NCPPHE) estimates that about half of all four-year college freshmen must take remedial classes. The NCPPHE pinpoints a flawed assumption:
Over the last 15 years, many states have emphasized mastery of specific content and performance standards, as shown through grades and statewide assessments; however, this shift to standards-based performance in the schools generally has not been extended to higher levels of achievement associated with college readiness, whose indicators still focus on courses taken. The flawed assumption has been that if students take the right courses and earn the right grades, they will be ready for college.[v]
We need to restore the legitimacy of college prep courses. Let’s ensure that all students who study and pass advanced subject matter have learned what that their parents, teachers and colleges assume they have learned.
To read more about the declining significance of coursetaking—and my thoughts on potential solutions to the problem in terms of algebra courses—please read the full paper, “The Algebra Imperative: Assessing Algebra in a National and International Context.”
[i] Elaine Allensworth, T. N. (2009). College Preparatory Curriculum for All: Academic Consequences of Requiring Algebra and English I for Ninth Graders in Chicago. Educational Evaluation and Policy Analysis, 31, 367. Jian-Hua Liang, P. E. (2012). What Do the California Standards Test Results Reveal About the Movement Toward Eighth-Grade Algebra for All? Educational Evaluation and Policy Analysis, 34 (3), 328-343. Charles T. Clotfelter, Helen F. Ladd, and Jacob L. Vigdor (2012), “The Aftermath of Accelerating Algebra: Evidence from a District Policy Initiative, http://www.newyorkfed.org/research/education_seminar_series/algebrapaper-011212.pdf
[ii] Brown, Janis, Kathryn Schiller, Stephen Roey, Robert Perkins, William Schmidt, and Richard Houang. Algebra I and Geometry: Results from the 2005 High School Transcript Mathematics Curriculum Study. Washington, DC: National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education, March 2013, 1.
[iii] Sparks, Sarah D. “Algebra, Geometry Classes Vary in Rigor, Say Study.” Education Week, March 27, 2013.
[iv] The California State University. Fall 2012 Final Regularly Admitted First-time Freshmen Remediation Systemwide. 2012. http://www.asd.calstate.edu/remediation/12/Rem_Sys_fall2012.htm.
[v] The National Center for Public Policy and Higher Education (2010). Beyond the Rhetoric: Improving College Readiness Through Coherent State Policy. http://www.highereducation.org/reports/college_readiness/CollegeReadiness.pdf




