This post discusses my monthly update of the Barnichon-Nekarda model. For an introduction to the basic concepts used in this post, read my introductory post (Full details are available here.)
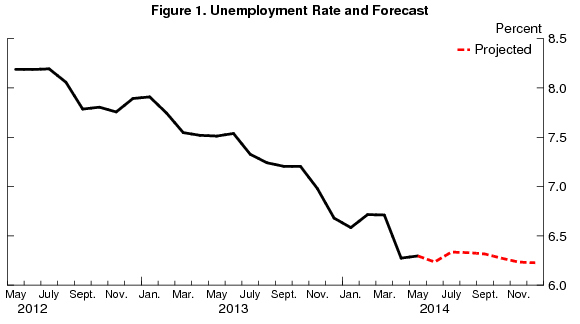
In May, the unemployment rate was steady at 6.3%, in line with last month’s forecast. Going forward, the contour of the forecast is unchanged with a steady unemployment rate over the next 6 months. I anticipate the unemployment rate to be unchanged at 6.3% in September and down to 6.2% by the end of the year.
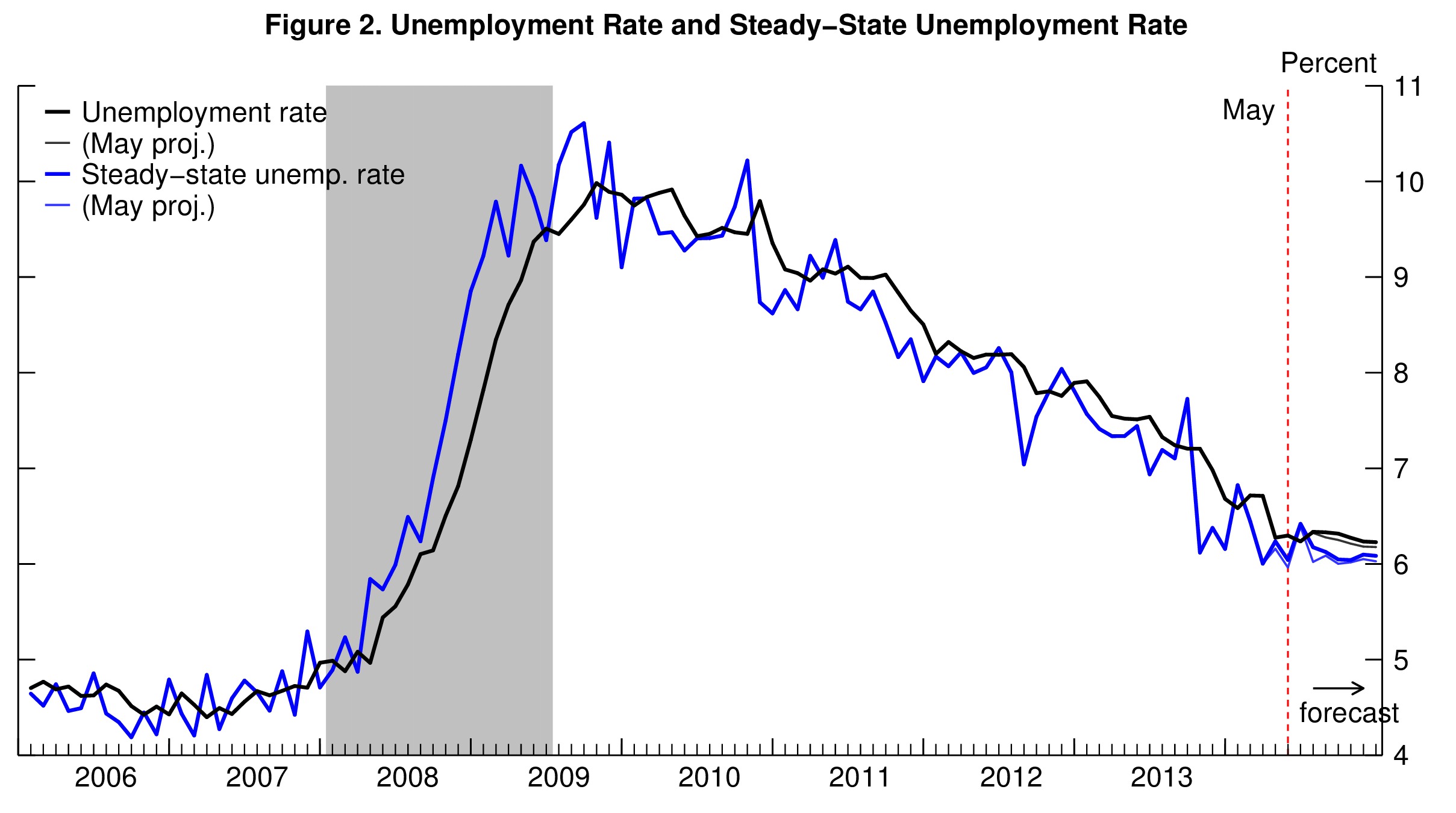
This model’s forecast can be easily understood by looking at the projected behavior of the “steady-state” unemployment rate. The steady-state unemployment rate, the rate of unemployment implied by the underlying labor force flows—the blue line in figure 2— stands currently at 6.4%, just 0.1% higher than the actual unemployment rate. Our research shows that the actual unemployment rate converges toward this steady state. With a steady-state unemployment rate slightly above the actual rate, the “steady-state convergence dynamic” would tend to push the unemployment rate up going forward. However, this effect is counter-balanced by an anticipated decline in the steady-state unemployment rate (SSUR) over the coming months with a steady-state rate of 6.1% by the end of the year (figure 2). Combining these two effects, the unemployment rate should remain roughly constant over next 6 months.
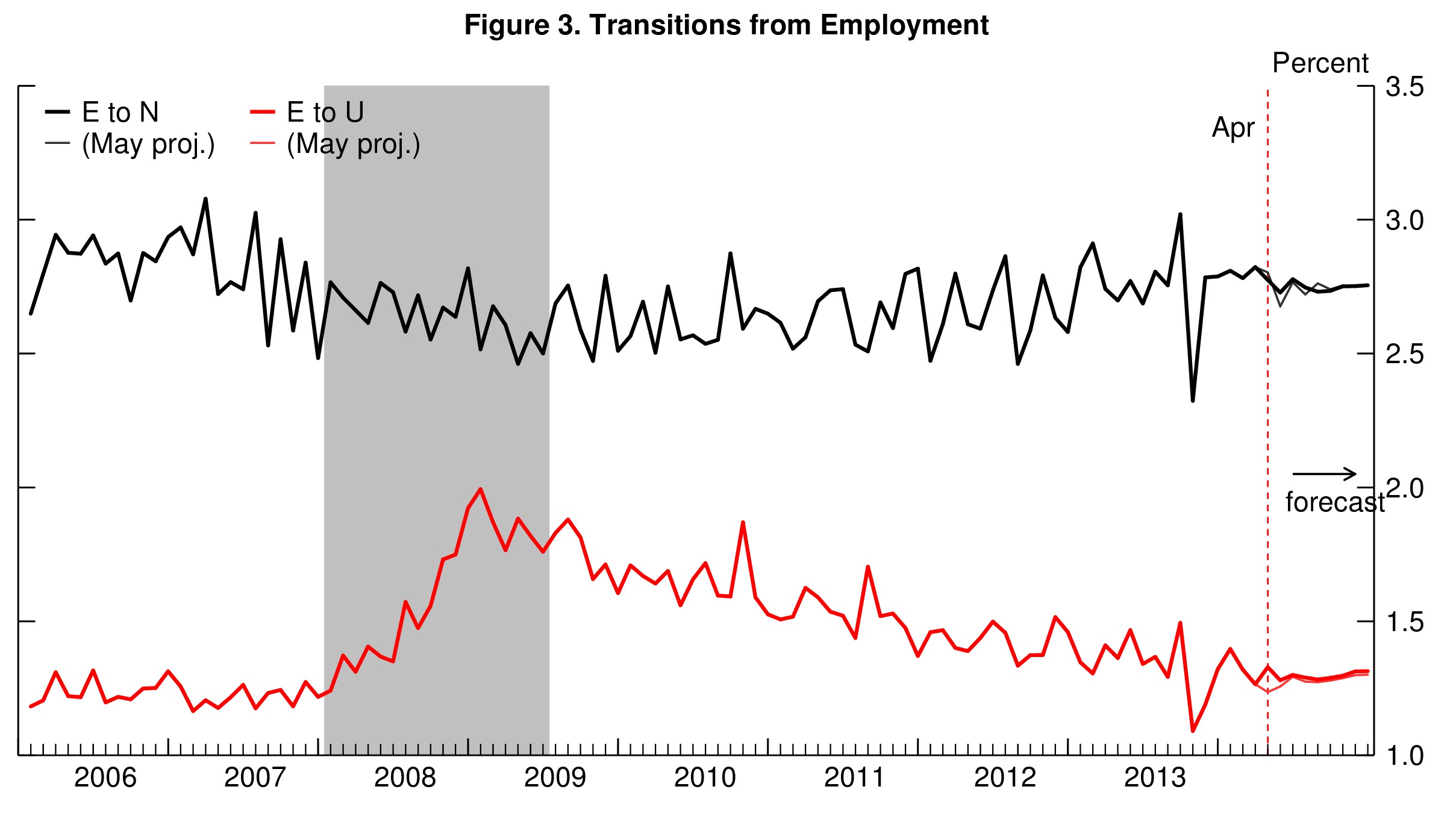
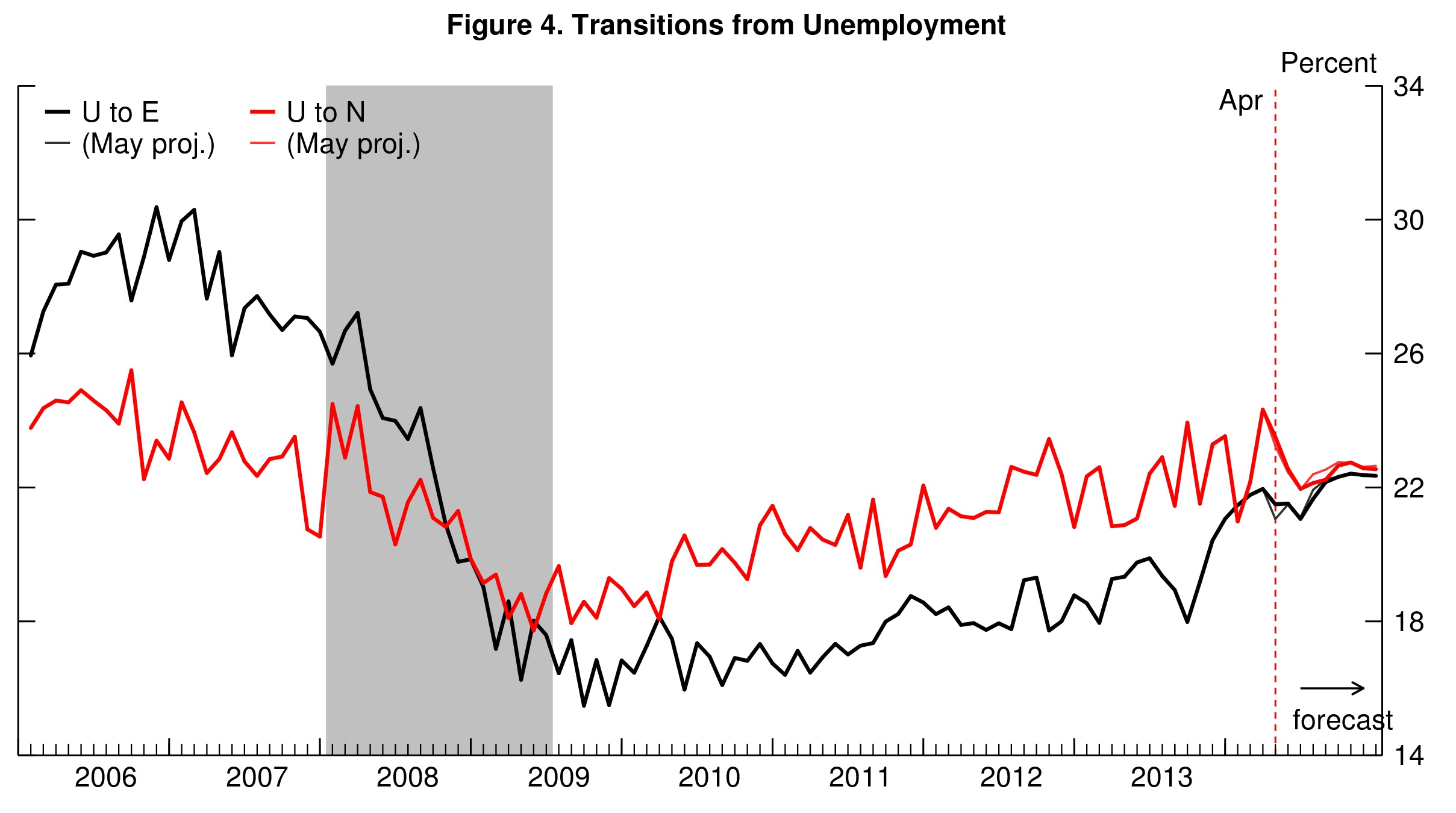
To forecast the behavior of steady-state unemployment, the model propagates forward its best estimate for how the flows in and out of unemployment will evolve over time. The forecasts for the flows are barely changed compared to last month. The job separation rate will remain roughly flat, being almost back at its pre-recession level (figure 3), but the job finding rate will increase in the last quarter of the year (figure 4), which will push down the steady-state unemployment rate.

To read more about the underlying model and the evidence that it outperforms other unemployment rate forecasts, see Barnichon and Nekarda (2012).



Commentary
Unemployment to Remain Steady Over the Next 6 Months
July 2, 2014