Measures matter when it comes to mobility. Yesterday we weighed the pro and cons of two persistence-based approaches: intergenerational elasticity of income (IGE) and rank-rank slope. Today we turn our attention to two movement-based measures: conditional transition mobility and directional rank mobility.
Conditional transition probability (CTP)
A clear picture can be drawn of where children born on different rungs of the income ladder end up as adults with a conditional transitional probabilities. What is the probability that a child born at a given percentile ends up at a different percentile as an adult? The specific approach that we use most often on this blog, and in our work as a whole, is a quintile transition matrix:
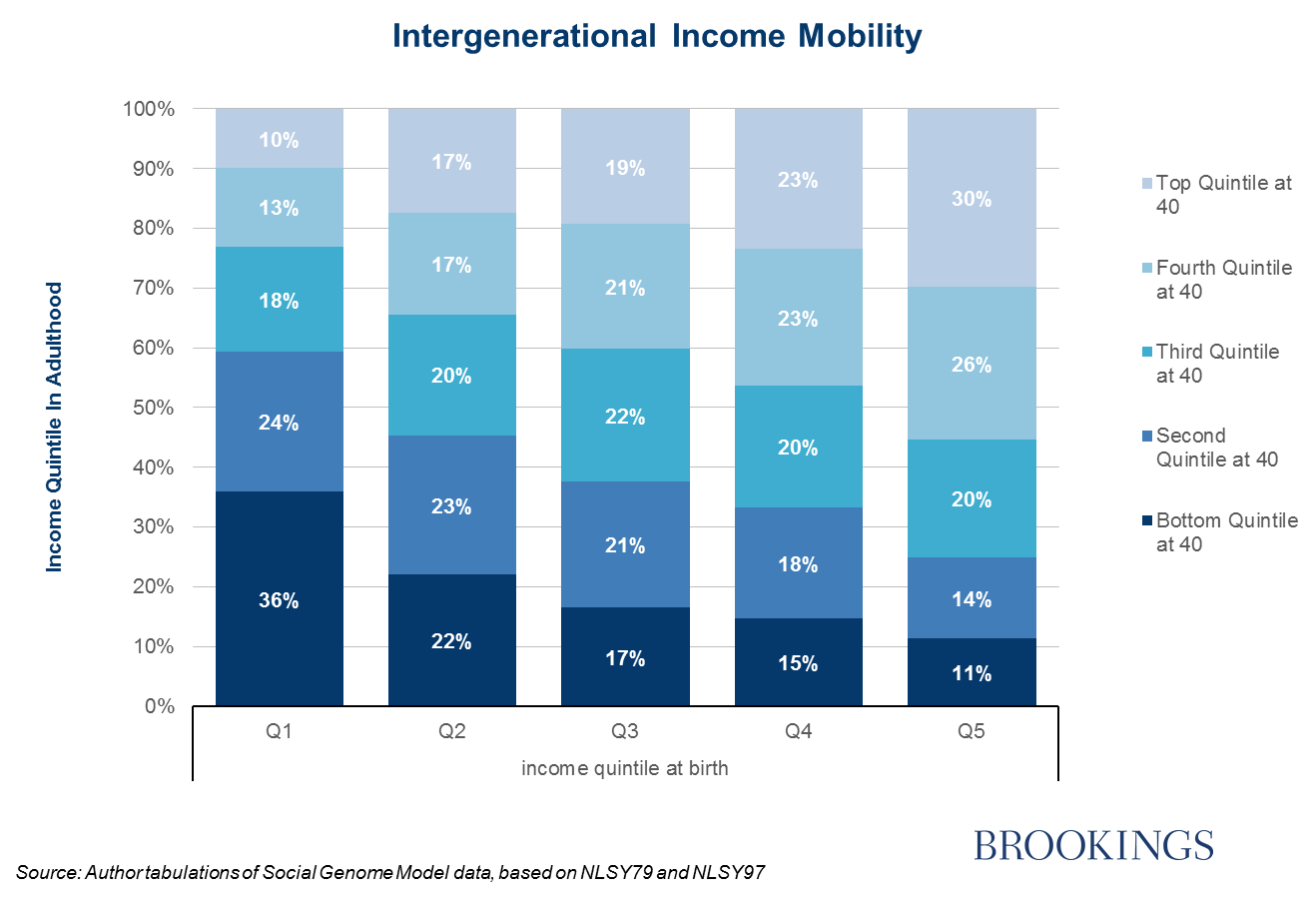
Typically, we use quintiles of the income distribution when discussing conditional relative mobility —for example, showing how likely it is that someone born in the bottom 20 percentiles will be in top 20 percentiles as an adult. But the approach can be applied to any preferred chunks of the income distribution: deciles, quartiles, terciles … take your pick.
The picture is clear but also dramatically simplified. Much of the variation in the degree of movement is lost. For example, if person A had a family income at the 19th percentile while person B’s was at the 12th percentile, both will start in the bottom quintile. But if both move up 5 percentiles as an adult, only one is categorized as ‘upwardly mobile,’ because the individual who started at the 12th percentile has not crossed the line into the second quintile.
Directional rank mobility (DRM)
Partly in response to this problem, economists Debopam Bhattacharya and Bhashkar Mazumder developed a new measure of mobility: directional rank mobility (DRM).This expresses the probability that a person’s percentile rank in the income distribution is a certain amount higher (or lower) than their parents income rank. DRM can be calculated across the distribution or for individuals at certain levels. Different degrees of movement can also be selected; for example, movements of more than 5, 10 or 20 percentiles can be calculated.
DRM is similar to conditional transition probabilities, in that it allows us to see the extent to which a person’s starting position on the income distribution is related to where they end up. But it does not suffer from the same sensitivity to the income level cut-offs. But what the DRM gains in sensitivity, it loses in simplicity. Transition matrices provide an ‘at a glance’ picture of mobility, including for different groups: DRM allows a more granular look.
First, choose the question; then choose your measure
The various kinds of measure for relative mobility, including the two discussed yesterday, are useful for different types of research and for answering different kinds of question. Relative mobility is not a singular concept. Researchers and pundits should define their terms clearly and select their measures carefully. Nor should we pretend that the selection of measures is a value-free process. In the end, what we choose to measure will reflect what we care most about, and there is no shame in that.


Commentary
Measuring relative mobility, part 2
April 28, 2015