
Part III of the 2015 Brown Center Report on American Education
Student engagement refers to the intensity with which students apply themselves to learning in school. Traits such as motivation, enjoyment, and curiosity—characteristics that have interested researchers for a long time—have been joined recently by new terms such as, “grit,” which now approaches cliché status. International assessments collect data from students on characteristics related to engagement. This study looks at data from the Program for International Student Assessment (PISA), an international test given to fifteen-year-olds. In the U.S., most PISA students are in the fall of their sophomore year. The high school years are a time when many observers worry that students lose interest in school.
Compared to their peers around the world, how do U.S. students appear on measures of engagement? Are national indicators of engagement related to achievement? This analysis concludes that American students are about average in terms of engagement. Data reveal that several countries noted for their superior ranking on PISA—e.g., Korea, Japan, Finland, Poland, and the Netherlands—score below the U.S. on measures of student engagement. Thus, the relationship of achievement to student engagement is not clear cut, with some evidence pointing toward a weak positive relationship and other evidence indicating a modest negative relationship.
The Unit of Analysis Matters
Education studies differ in units of analysis. Some studies report data on individuals, with each student serving as an observation. Studies of new reading or math programs, for example, usually report an average gain score or effect size representing the impact of the program on the average student. Others studies report aggregated data, in which test scores or other measurements are averaged to yield a group score. Test scores of schools, districts, states, or countries are constructed like that. These scores represent the performance of groups, with each group serving as a single observation, but they are really just data from individuals that have been aggregated to the group level.
Aggregated units are particularly useful for policy analysts. Analysts are interested in how Fairfax County or the state of Virginia or the United States is doing. Governmental bodies govern those jurisdictions and policymakers craft policy for all of the citizens within the political jurisdiction—not for an individual.
The analytical unit is especially important when investigating topics like student engagement and their relationships with achievement. Those relationships are inherently individual, focusing on the interaction of psychological characteristics. They are also prone to reverse causality, meaning that the direction of cause and effect cannot readily be determined. Consider self-esteem and academic achievement. Determining which one is cause and which is effect has been debated for decades. Students who are good readers enjoy books, feel pretty good about their reading abilities, and spend more time reading than other kids. The possibility of reverse causality is one reason that beginning statistics students learn an important rule: correlation is not causation.
Starting with the first international assessments in the 1960s, a curious pattern has emerged. Data on students’ attitudes toward studying school subjects, when examined on a national level, often exhibit the opposite relationship with achievement than one would expect. The 2006 Brown Center Report (BCR) investigated the phenomenon in a study of “the happiness factor” in learning.[i] Test scores of fourth graders in 25 countries and eighth graders in 46 countries were analyzed. Students in countries with low math scores were more likely to report that they enjoyed math than students in high-scoring countries. Correlation coefficients for the association of enjoyment and achievement were -0.67 at fourth grade and -0.75 at eighth grade.
Confidence in math performance was also inversely related to achievement. Correlation coefficients for national achievement and the percentage of students responding affirmatively to the statement, “I usually do well in mathematics,” were -0.58 among fourth graders and -0.64 among eighth graders. Nations with the most confident math students tend to perform poorly on math tests; nations with the least confident students do quite well.
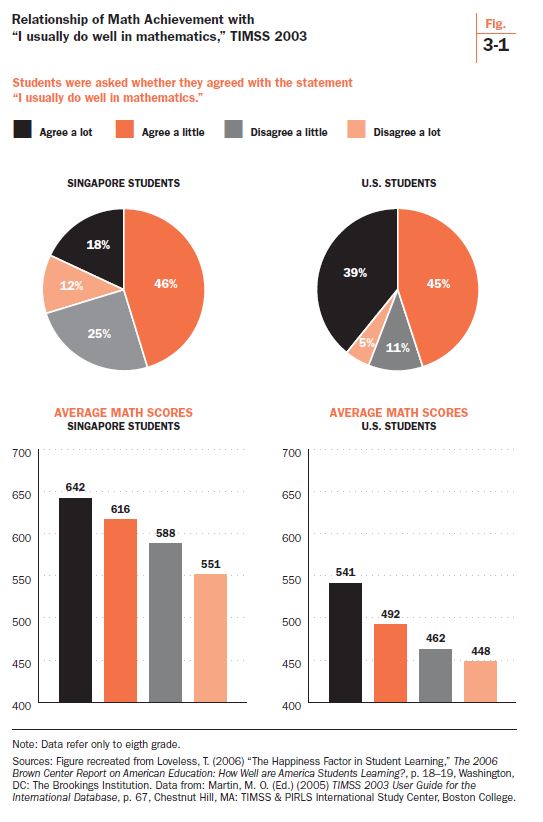
That is odd. What’s going on? A comparison of Singapore and the U.S. helps unravel the puzzle. The data in figure 3-1 are for eighth graders on the 2003 Trends in Mathematics and Science Study (TIMSS). U.S. students were very confident—84% either agreed a lot or a little (39% + 45%) with the statement that they usually do well in mathematics. In Singapore, the figure was 64% (46% + 18%). With a score of 605, however, Singaporean students registered about one full standard deviation (80 points) higher on the TIMSS math test compared to the U.S. score of 504.
When within-country data are examined, the relationship exists in the expected direction. In Singapore, highly confident students score 642, approximately 100 points above the least-confident students (551). In the U.S., the gap between the most- and least-confident students was also about 100 points—but at a much lower level on the TIMSS scale, at 541 and 448. Note that the least-confident Singaporean eighth grader still outscores the most-confident American, 551 to 541.
The lesson is that the unit of analysis must be considered when examining data on students’ psychological characteristics and their relationship to achievement. If presented with country-level associations, one should wonder what the within-country associations are. And vice versa. Let’s keep that caution in mind as we now turn to data on fifteen-year-olds’ intrinsic motivation and how nations scored on the 2012 PISA.
Intrinsic Motivation
PISA’s index of intrinsic motivation to learn mathematics comprises responses to four items on the student questionnaire: 1) I enjoy reading about mathematics; 2) I look forward to my mathematics lessons; 3) I do mathematics because I enjoy it; and 4) I am interested in the things I learn in mathematics. Figure 3-2 shows the percentage of students in OECD countries—thirty of the most economically developed nations in the world—responding that they agree or strongly agree with the statements. A little less than one-third (30.6%) of students responded favorably to reading about math, 35.5% responded favorably to looking forward to math lessons, 38.2% reported doing math because they enjoy it, and 52.9% said they were interested in the things they learn in math. A ballpark estimate, then, is that one-third to one-half of students respond affirmatively to the individual components of PISA’s intrinsic motivation index.
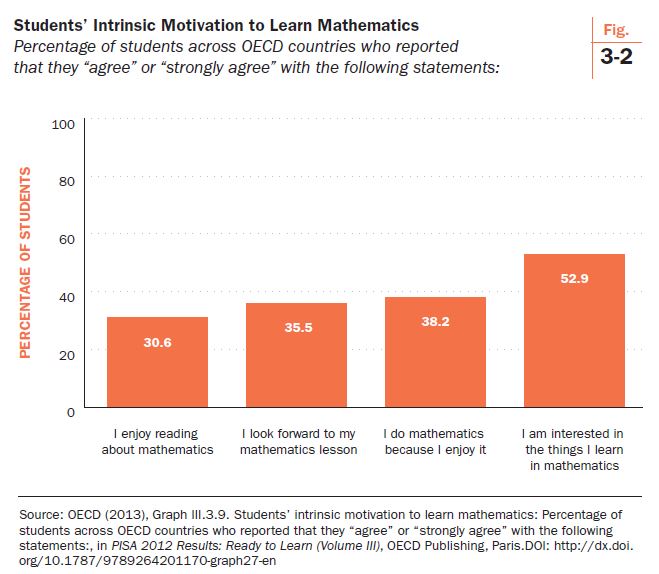
Table 3-1 presents national scores on the 2012 index of intrinsic motivation to learn mathematics. The index is scaled with an average of 0.00 and a standard deviation of 1.00. Student index scores are averaged to produce a national score. The scores of 39 nations are reported—29 OECD countries and 10 partner countries.[ii] Indonesia appears to have the most intrinsically motivated students in the world (0.80), followed by Thailand (0.77), Mexico (0.67), and Tunisia (0.59). It is striking that developing countries top the list. Universal education at the elementary level is only a recent reality in these countries, and they are still struggling to deliver universally accessible high schools, especially in rural areas and especially to girls. The students who sat for PISA may be an unusually motivated group. They also may be deeply appreciative of having an opportunity that their parents never had.
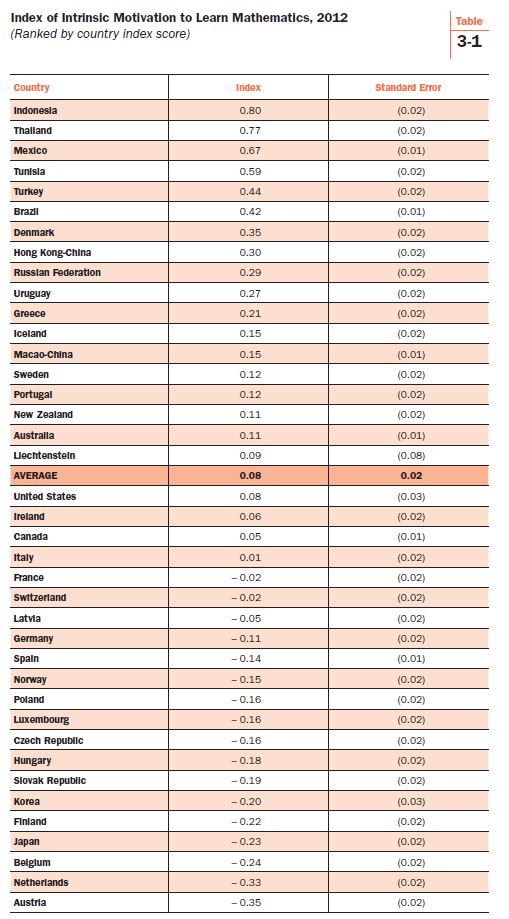
The U.S. scores about average (0.08) on the index, statistically about the same as New Zealand, Australia, Ireland, and Canada. The bottom of the table is extremely interesting. Among the countries with the least intrinsically motivated kids are some PISA high flyers. Austria has the least motivated students (-0.35), but that is not statistically significantly different from the score for the Netherlands (-0.33). What’s surprising is that Korea (-0.20), Finland (-0.22), Japan (-0.23), and Belgium (-0.24) score at the bottom of the intrinsic motivation index even though they historically do quite well on the PISA math test.
Enjoying Math and Looking Forward to Math Lessons
Let’s now dig a little deeper into the intrinsic motivation index. Two components of the index are how students respond to “I do mathematics because I enjoy it” and “I look forward to my mathematics lessons.” These sentiments are directly related to schooling. Whether students enjoy math or look forward to math lessons is surely influenced by factors such as teachers and curriculum. Table 3-2 rank orders PISA countries by the percentage of students who “agree” or “strongly agree” with the questionnaire prompts. The nations’ 2012 PISA math scores are also tabled. Indonesia scores at the top of both rankings, with 78.3% enjoying math and 72.3% looking forward to studying the subject. However, Indonesia’s PISA math score of 375 is more than one full standard deviation below the international mean of 494 (standard deviation of 92). The tops of the tables are primarily dominated by low-performing countries, but not exclusively so. Denmark is an average-performing nation that has high rankings on both sentiments. Liechtenstein, Hong Kong-China, and Switzerland do well on the PISA math test and appear to have contented, positively-oriented students.
Several nations of interest are shaded. The bar across the middle of the tables, encompassing Australia and Germany, demarcates the median of the two lists, with 19 countries above and 19 below that position. The United States registers above the median on looking forward to math lessons (45.4%) and a bit below the median on enjoyment (36.6%). A similar proportion of students in Poland—a country recently celebrated in popular media and in Amanda Ripley’s book, The Smartest Kids in the World,[iii] for making great strides on PISA tests—enjoy math (36.1%), but only 21.3% of Polish kids look forward to their math lessons, very near the bottom of the list, anchored by Netherlands at 19.8%.
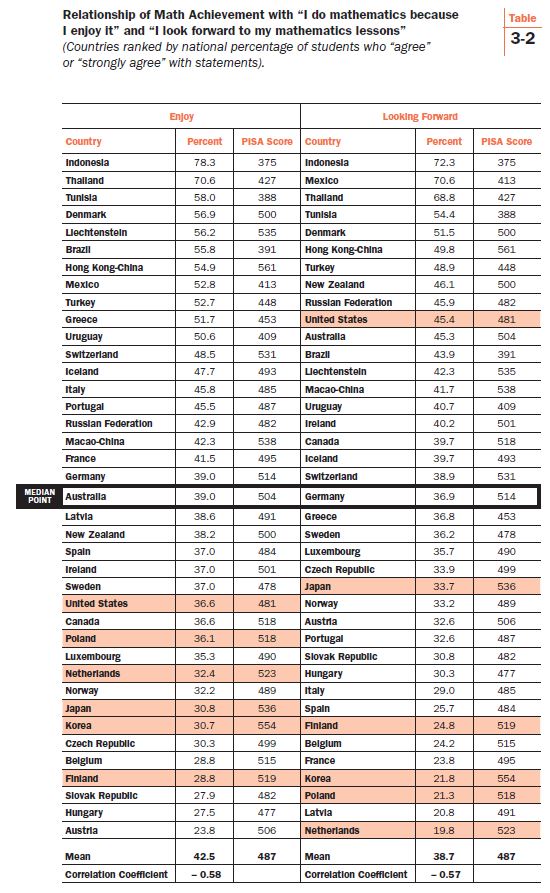
Korea also appears in Ripley’s book. It scores poorly on both items. Only 30.7% of Korean students enjoy math, and less than that, 21.8%, look forward to studying the subject. Korean education is depicted unflatteringly in Ripley’s book—as an academic pressure cooker lacking joy or purpose—so its standing here is not surprising. But Finland is another matter. It is portrayed as laid-back and student-centered, concerned with making students feel relaxed and engaged. Yet, only 28.8% of Finnish students say that they study mathematics because they enjoy it (among the bottom four countries) and only 24.8% report that they look forward to math lessons (among the bottom seven countries). Korea, the pressure cooker, and Finland, the laid-back paradise, look about the same on these dimensions.
Another country that is admired for its educational system, Japan, does not fare well on these measures. Only 30.8% of students in Japan enjoy mathematics, despite the boisterous, enthusiastic classrooms that appear in Elizabeth Green’s recent book, Building a Better Teacher.[iv] Japan does better on the percentage of students looking forward to their math lessons (33.7%), but still places far below the U.S. Green’s book describes classrooms with younger students, but even so, surveys of Japanese fourth and eighth graders’ attitudes toward studying mathematics report results similar to those presented here. American students say that they enjoy their math classes and studying math more than students in Finland, Japan, and Korea.
It is clear from Table 3-2 that at the national level, enjoying math is not positively related to math achievement. Nor is looking forward to one’s math lessons. The correlation coefficients reported in the last row of the table quantify the magnitude of the inverse relationships. The -0.58 and -0.57 coefficients indicate a moderately negative association, meaning, in plain English, that countries with students who enjoy math or look forward to math lessons tend to score below average on the PISA math test. And high-scoring nations tend to register below average on these measures of student engagement. Country-level associations, however, should be augmented with student-level associations that are calculated within each country.
Within-Country Associations of Student Engagement with Math Performance
The 2012 PISA volume on student engagement does not present within-country correlation coefficients on intrinsic motivation or its components. But it does offer within-country correlations of math achievement with three other characteristics relevant to student engagement. Table 3-3 displays statistics for students’ responses to: 1) if they feel like they belong at school; 2) their attitudes toward school, an index composed of four factors;[v] and 3) whether they had arrived late for school in the two weeks prior to the PISA test. These measures reflect an excellent mix of behaviors and dispositions.
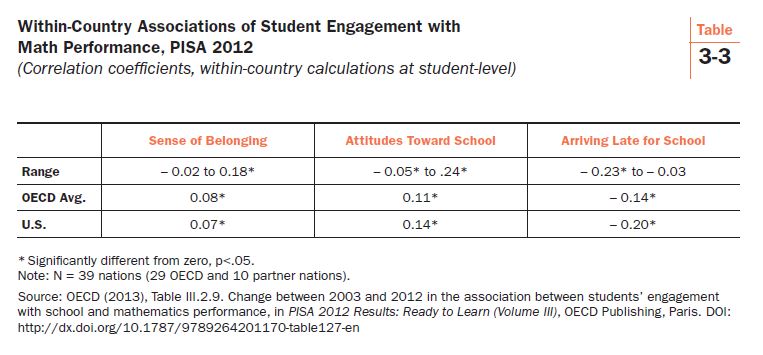
The within-country correlations trend in the direction expected but they are small in magnitude. Correlation coefficients for math performance and a sense of belonging at school range from -0.02 to 0.18, meaning that the country exhibiting the strongest relationship between achievement and a sense of belonging—Thailand, with a 0.18 correlation coefficient—isn’t registering a strong relationship at all. The OECD average is 0.08, which is trivial. The U.S. correlation coefficient, 0.07, is also trivial. The relationship of achievement with attitudes toward school is slightly stronger (OECD average of 0.11), but is still weak.
Of the three characteristics, arriving late for school shows the strongest correlation, an unsurprising inverse relationship of -0.14 in OECD countries and -0.20 in the U.S. Students who tend to be tardy also tend to score lower on math tests. But, again, the magnitude is surprisingly small. The coefficients are statistically significant because of large sample sizes, but in a real world “would I notice this if it were in my face?” sense, no, the correlation coefficients are suggesting not much of a relationship at all.
The PISA report presents within-country effect sizes for the intrinsic motivation index, calculating the achievement gains associated with a one unit change in the index. One of several interesting findings is that intrinsic motivation is more strongly associated with gains at the top of the achievement distribution, among students at the 90th percentile in math scores, than at the bottom of the distribution, among students at the 10th percentile.
The report summarizes the within-country effect sizes with this statement: “On average across OECD countries, a change of one unit in the index of intrinsic motivation to learn mathematics translates into a 19 score-point difference in mathematics performance.”[vi] This sentence can be easily misinterpreted. It means that within each of the participating countries students who differ by one unit on PISA’s 2012 intrinsic motivation index score about 19 points apart on the 2012 math test. It does not mean that a country that gains one unit on the intrinsic motivation index can expect a 19 point score increase.[vii]
Let’s now see what that association looks like at the national level.
National Changes in Intrinsic Motivation, 2003-2012
PISA first reported national scores on the index of intrinsic motivation to learn mathematics in 2003. Are gains that countries made on the index associated with gains on PISA’s math test? Table 3-4 presents a score card on the question, reporting the changes that occurred in thirty-nine nations—in both the index and math scores—from 2003 to 2012. Seventeen nations made statistically significant gains on the index; fourteen nations had gains that were, in a statistical sense, indistinguishable from zero—labeled “no change” in the table; and eight nations experienced statistically significant declines in index scores.
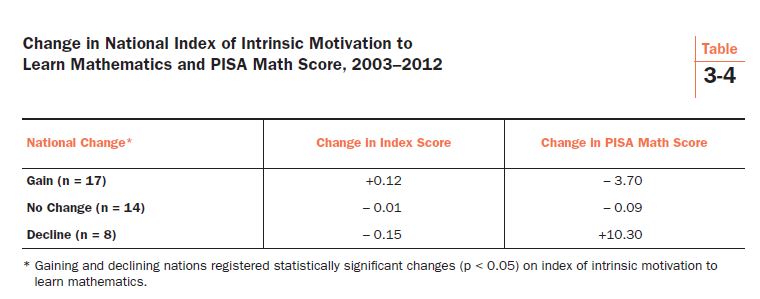
The U.S. scored 0.00 in 2003 and 0.08 in 2012, notching a gain of 0.08 on the index (statistically significant). Its PISA math score declined from 483 to 481, a decline of 2 scale score points (not statistically significant).
Table 3-4 makes it clear that national changes on PISA’s intrinsic motivation index are not associated with changes in math achievement. The countries registering gains on the index averaged a decline of 3.7 points on PISA’s math assessment. The countries that remained about the same on the index had math scores that also remain essentially unchanged (-0.09) And the most striking finding: countries that declined on the index (average of -0.15) actually gained an average of 10.3 points on the PISA math scale. Intrinsic motivation went down; math scores went up. The correlation coefficient for the relationship over all, not shown in the table, is -0.30.
Conclusion
The analysis above investigated student engagement. International data from the 2012 PISA were examined on several dimensions of student engagement, focusing on a measure that PISA has employed since 2003, the index of intrinsic motivation to learn mathematics. The U.S. scored near the middle of the distribution on the 2012 index. PISA analysts calculated that, on average, a one unit change in the index was associated with a 19 point gain on the PISA math test. That is the average of within-country calculations, using student-level data that measure the association of intrinsic motivation with PISA score. It represents an effect size of about 0.20—a positive effect, but one that is generally considered small in magnitude.[viii]
The unit of analysis matters. Between-country associations often differ from within-country associations. The current study used a difference in difference approach that calculated the correlation coefficient for two variables at the national level: the change in intrinsic motivation index from 2003-2012 and change in PISA score for the same time period. That analysis produced a correlation coefficient of -0.30, a negative relationship that is also generally considered small in magnitude.
Neither approach can justify causal claims nor address the possibility of reverse causality occurring—the possibility that high math achievement boosts intrinsic motivation to learn math, rather than, or even in addition to, high levels of motivation leading to greater learning. Poor math achievement may cause intrinsic motivation to fall. Taken together, the analyses lead to the conclusion that PISA provides, at best, weak evidence that raising student motivation is associated with achievement gains. Boosting motivation may even produce declines in achievement.
Here’s the bottom line for what PISA data recommends to policymakers: Programs designed to boost student engagement—perhaps a worthy pursuit even if unrelated to achievement—should be evaluated for their effects in small scale experiments before being adopted broadly. The international evidence does not justify wide-scale concern over current levels of student engagement in the U.S. or support the hypothesis that boosting student engagement would raise student performance nationally.
Let’s conclude by considering the advantages that national-level, difference in difference analyses provide that student-level analyses may overlook.
1. They depict policy interventions more accurately. Policies are actions of a political unit affecting all of its members. They do not simply affect the relationship of two characteristics within an individual’s psychology. Policymakers who ask the question, “What happens when a country boosts student engagement?” are asking about a country-level phenomenon.
2. Direction of causality can run differently at the individual and group levels. For example, we know that enjoying a school subject and achievement on tests of that subject are positively correlated at the individual level. But they are not always correlated—and can in fact be negatively correlated—at the group level.
3. By using multiple years of panel data and calculating change over time, a difference in difference analysis controls for unobserved variable bias by “baking into the cake” those unobserved variables at the baseline. The unobserved variables are assumed to remain stable over the time period of the analysis. For the cultural factors that many analysts suspect influence between-nation test score differences, stability may be a safe assumption. Difference in difference, then, would be superior to cross-sectional analyses in controlling for cultural influences that are omitted from other models.
4. Testing artifacts from a cultural source can also be dampened. Characteristics such as enjoyment are culturally defined, and the language employed to describe them is also culturally bounded. Consider two of the questionnaire items examined above: whether kids “enjoy” math and how much they “look forward” to math lessons. Cultural differences in responding to these prompts will be reflected in between-country averages at the baseline, and any subsequent changes will reflect fluctuations net of those initial differences.
[i] Tom Loveless, “The Happiness Factor in Student Learning,” The 2006 Brown Center Report on American Education: How Well are American Students Learning? (Washington, D.C.: The Brookings Institution, 2006).
[ii] All countries with 2003 and 2012 data are included.
[iii] Amanda Ripley, The Smartest Kids in the World: And How They Got That Way (New York, NY: Simon & Schuster, 2013)
[iv] Elizabeth Green, Building a Better Teacher: How Teaching Works (and How to Teach It to Everyone) (New York, NY: W.W. Norton & Company, 2014).
[v] The attitude toward school index is based on responses to: 1) Trying hard at school will help me get a good job, 2) Trying hard at school will help me get into a good college, 3) I enjoy receiving good grades, 4) Trying hard at school is important. See: OECD, PISA 2012 Database, Table III.2.5a.
[vi] OECD, PISA 2012 Results: Ready to Learn: Students’ Engagement, Drive and Self-Beliefs (Volume III) (Paris: PISA, OECD Publishing, 2013), 77.
[vii] PISA originally called the index of intrinsic motivation the index of interest and enjoyment in mathematics, first constructed in 2003. The four questions comprising the index remain identical from 2003 to 212, allowing for comparability. Index values for 2003 scores were re-scaled based on 2012 scaling (mean of 0.00 and SD of 1.00), meaning that index values published in PISA reports prior to 2012 will not agree with those published after 2012 (including those analyzed here). See: OECD, PISA 2012 Results: Ready to Learn: Students’ Engagement, Drive and Self-Beliefs (Volume III) (Paris: PISA, OECD Publishing, 2013), 54.
[viii] PISA math scores are scaled with a standard deviation of 100, but the average within-country standard deviation for OECD nations was 92 on the 2012 math test.
| « Part II: Measuring Effects of the Common Core |
The Brookings Institution is committed to quality, independence, and impact.
We are supported by a diverse array of funders. In line with our values and policies, each Brookings publication represents the sole views of its author(s).




