When NASA began planning a manned flight to the moon, their rocket scientists did a few calculations. They realized that incremental improvements in rocket design would not provide enough lift. Whereas the Jupiter series of rockets had a payload capacity of 11 kilograms, the new rockets would require a payload 10,000 times greater (to carry all the extra equipment manned flight would require). In the end, the Saturn V rocket was dramatically different from previous rocket designs—because it had to be. At 360 feet in height, it stood more than five times taller, five times wider and 100 times heavier than the Jupiter rockets that preceded it.
In education, we never bother to calculate the thrust needed to carry our schools to our stated targets. Too often, we draw up proposals which are directionally correct: better professional development for teachers, higher teacher salaries, incrementally smaller class sizes, better facilities, stronger broad-band connections for schools, etc. However, we do not pause long enough to consult the evidence on expected effect sizes and assemble a list of reforms that could plausibly succeed in achieving our ambitious goals. When we fail to right-size our reform efforts, we breed a sense of futility among teachers, parents and policymakers. We might as well be shooting bottle rockets at the moon.
Let’s take a goal often repeated by our political leaders: closing the gap with top-performing nations on international assessments. What do we really think will be required to achieve such a goal?
Figure 1 displays mean scores on the PISA math assessment in 2012 against GDP per capita in each country. On PISA, the U.S. mean score is 75 points lower than the mean of top-performing countries (Korea, Taiwan, Hong Kong, Singapore and Japan). It has been difficult to translate that gap into a measure that makes sense in the U.S. context. One approach is to convert the gap into standard deviations of U.S. student performance. The standard deviation in PISA math scores in the U.S. is 90. Therefore, the gap between the U.S. and the top performing countries is equivalent to .83 standard deviations in the scores of individual students in the U.S.
Figure 1.
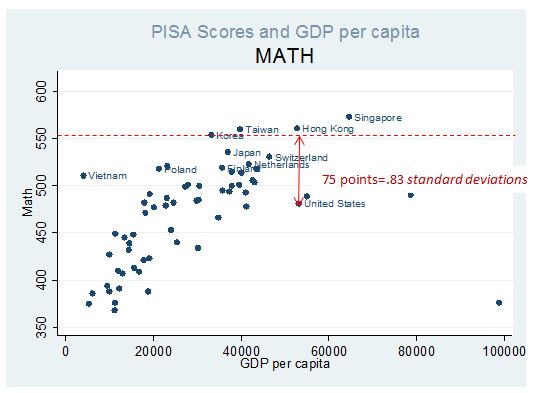
That’s a quantity we should be able to understand, since it’s roughly equal to the gap in math scores between African American and white students in the U.S. It’s a gap our school systems have said they want to close for four decades. That history should tell us that it’s unrealistic to expect to close such a large gap in a single year. Instead, suppose we were to aim to close the gap between the U.S. and top-performing countries for the 15-year-olds taking the PISA in 2024—ten years from now. How might we produce ten straight years of additional gains of .08 student-level standard deviations so that the cohort of 15-year-olds in 2024 achieves what the top-performing countries are achieving now?
The Expected Thrust from the Current Reform Agenda
There is reason to hope that the current reform efforts—if sustained—could provide the needed thrust to produce the necessary gains over the next decade. There are three key elements to those reforms: making better personnel decisions at tenure time; providing feedback to allow teachers to improve their practice; and more rigorous standards and assessments. A fourth element—a more personalized learning environment—also holds promise for improving productivity, but the evidence is still lacking.
Making Better Personnel Decisions: Evidence has long suggested that teacher effects are quite large and that a focus on identifying and rewarding effective teachers should pay off. But by how much? One standard deviation in teacher effects in math is in the range of .15 student-level standard deviations in most districts. We have only imperfect measures of teachers’ effectiveness and, with one year of data, the variance in the estimation error can be as large as the variance in underlying teacher effects. Estimation error will dampen the effect of any effort to retain effective teachers, since some of those identified as “effective” will not be, and some of those who were deemed “ineffective” will be unfairly categorized. Suppose the available measure were equal parts signal and noise, each with a standard deviation of .15. If the bottom 25 percent of teachers on such a measure were not retained, we would expect average student achievement to rise by .09 student-level standard deviations. If there were no fade-out of teacher effects, a policy of retaining only the top 75 percent of teachers at tenure time puts us on the path to closing the gap with the top-performing countries within ten years. However, accounting for fade-out in teacher effects would roughly cut that number in half to .045 standard deviations.
Providing Better Feedback to Teachers: There is also evidence that giving teachers feedback from high quality classroom observations leads to subsequent improvements in their students’ achievement. Eric Taylor and John Tyler have reported that providing teachers with feedback from classroom observations in Cincinnati led to a .10 student-level standard deviation improvement in teacher effects. That seems large. Given the current focus on classroom observations around the country, we should learn soon if those results can be replicated. But suppose it is half that large, .05 student-level standard deviations. After accounting for fade-out, that would produce an additional .025 standard deviations per year.
More Rigorous Standards and Assessments: What magnitude rise could we hope for with the transition to the Common Core? Although the Massachusetts education reform law of 1993 dramatically raised state spending in low-income districts and launched the development of new state standards, the new test embodying the standards was not administered until the spring of 1999. That’s when the “Massachusetts miracle” seems to have started. Figure 2 portrays the trend in NAEP scores in Massachusetts versus the national trend in fourth and eighth grade mathematics from 1992 through 2013. Although the state diverted enormous resources to low-income districts between 1992 and 2000, Massachusetts essentially followed the national trend during that time period. Only after the MCAS test was introduced did scores begin to rise in Massachusetts relative to the nation as a whole. The gap in fourth grade math was seven points in 2000 and grew to 12 points by 2007. One might take that “difference in the difference” between Massachusetts and the national trend between 2000 and 2007 as an estimate of the improvement attributable to the more demanding standards in Massachusetts. The five point widening of the Massachusetts advantage between 2000 and 2007 is approximately .17 standard deviations. Spread across seven years, that amounts to .024 standard deviations per year.
Figure 2 reports similar trends for eighth grade mathematics. The difference in scores between Massachusetts and the national average grew from six points to 16 points between 2000 and 2007, after which the gap stopped increasing. That is almost .04 standard deviations per year in eighth grade math.
Figure 2.
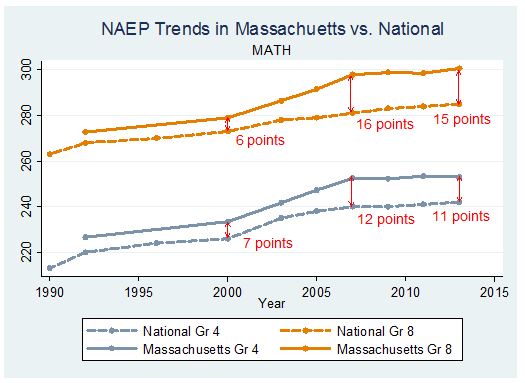
Both trends seemed to top out after 2007, so higher standards do not lead to a permanent change in achievement gains per grade level (as would be expected to happen with a permanent change in the quality of teaching).
Actual Improvements Since 2000
Obviously, it remains to be seen if the predicted improvements are borne out in the years ahead. Nevertheless, the experience in Washington, DC public schools provides reason for hope.
In the years immediately following the No Child Left Behind Act (2002 to 2005), about half of all states improved their average fourth grade math achievement on NAEP at a rate faster than .08 standard deviations per year (which translates to 2.3 NAEP points).[1] However, based on my calculations with state NAEP data, only Arizona and the District of Columbia were able to sustain such a rate of improvement over a period of four or more years after 2005 (between 2009 and 2013 in Arizona and between 2007 and 2013 in the District).
It has been much harder to show similar gains in eighth grade math. South Carolina did so between 2000 and 2005. And the District of Columbia did so between 2007 and 2011.
That means that only the District of Columbia has ever raised performance by more than .08 standard deviations per year in both fourth grade and eighth grade math over a period of four or more years. This was achieved under the leadership of Michelle Rhee and Kaya Henderson. Despite the controversy their work has occasionally engendered, the District of Columbia is demonstrating the type of sustained achievement growth our nation will need in order to catch up with the top-performing countries.
Figure 3 compares the improvements in fourth and eighth grade NAEP in DC to the nation as a whole. Between 2000 and 2007, scores were improving in DC as well as the nation as a whole. The gap in mean scores fell by eight points in fourth grade and by five points in eighth grade. However, when improvements flattened out nationally after 2007, the improvements in DC accelerated. The gap between DC and the nation on both the fourth grade and eighth grade assessments narrowed by 13 points between 2007 and 2013.
Figure 3.
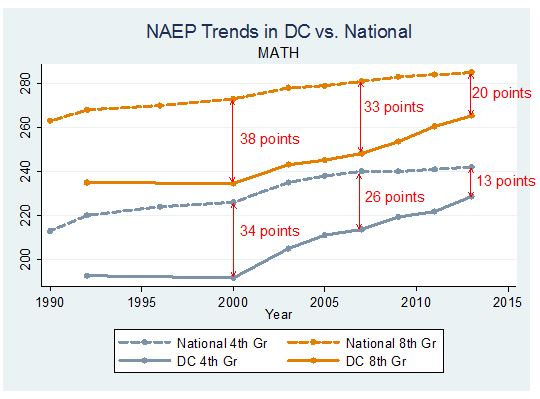
Putting it All Together
Summing up the above estimates, we might expect .045 standard deviations per year in achievement gains from more selective personnel decisions, .025 standard deviations per year from better feedback for teachers and between .024 and .040 standard deviations per year from the higher standards. In sum, they would produce .09 to .11 standard deviations per year. Gains of that magnitude would put us on course to close the gap with the top-scoring PISA countries within ten years.
There is evidence suggesting that there may be other ways to close the gap. For instance, Roland Fryer worked with the Houston school district to study the impact of implementing a package of changes drawn from effective charter schools in a set of traditional public schools in Houston. They randomly assigned nine of 18 low-achieving elementary schools to receive a package of reforms: new school leadership, selective retention of teaching staff based on prior evaluations (including value-added), providing better feedback to teachers, a longer school day and year, intensive tutoring, and data-driven instruction. Relative to the comparison schools, the interventions raised achievement in math by .10 standard deviations per year—in line with the hypothetical estimates above. However, such reforms would not be uncontroversial either.
Before setting off, we must be able to make a plausible argument that a given set of reforms will produce improvements of the desired magnitude. There is no reason to expect that non-controversial, incremental policies such as more professional development, incrementally smaller class sizes, and better facilities will produce substantial change. The current backlash against the Common Core and new teacher evaluation systems is, at least in part, a result of our long history of underpowered, incremental reforms. By failing to worry about magnitudes, we have led politicians and voters to expect school reform without controversy. We cannot return to shooting bottle rockets when Saturn V’s are required. We need to recognize the magnitude of the changes required to achieve our goals.
[1] Arkansas, California, District of Columbia, Georgia, Hawaii, Idaho, Kansas, Kentucky, Louisiana, Maryland, Massachusetts, Minnesota, Mississippi, Montana, Nebraska, New York, North Dakota, Ohio, Oregon, South Carolina, Tennessee, Utah, Vermont and Wyoming.



