A nasty political fight between New York Governor Andrew Cuomo and the state teachers’ union has embroiled the state since Cuomo announced a set of education policy proposals in January that led the state’s union president to declare that Cuomo had “declared war on the public schools.” In the end, Cuomo got much (but not all) of what he wanted, including changes to teacher evaluation and tenure policies, which the State Senate and Assembly approved last month.
The state teachers’ union has not taken defeat lying down, responding in part by encouraging parents to “opt-out” their children from the standardized exams that are used as a factor in the evaluation system. Union president Karen Magee argued that a large number of opt-outs could sabotage the evaluation system: “Statistically, if you take out enough, it has no merit or value whatsoever.”
Is Magee’s statistical argument correct? Taken to enough of an extreme, it surely is. If all students opted out, there would be no test data to include in teacher evaluations. But what would be the likely impact of some, or even many, but not all students refusing to take the tests? My colleague Katharine Lindquist and I used statewide data from North Carolina to simulate the impact of opt-out on test-score-based measures of teacher performance.[1] We ran two sets of simulations: one where students opt-out randomly, and another in which opt-out occurs among the highest-performing students in each classroom (as measured by their prior test scores).
Opting out adds noise to the data, which increases the amount of variability in the teacher performance measures because each teacher’s score is based on fewer students. A teacher faces a higher risk of being labelled low-performing (or high-performing) as the number of opt-outs in her classroom increases. But the effect of opt-out is quite small unless a large number of students do so.
A teacher in New York State is considered to be ineffective based on her students’ test score growth if her value-added score is more than 1.5 standard deviations below average (i.e., in the bottom seven percent of teachers). If a handful of students opt out, little changes. The risk of getting the lowest score barely changes even if five students in the class opt out—more than 20 percent of the typical classroom.
But if enough of a teacher’s students opt out, her risk of getting a bad score increases.[2] For example, imagine a teacher who strongly encourages her students to opt out of the tests and succeeds in getting 15 students—a majority of the class—to opt out. That teacher would have a significantly elevated risk of getting an ineffective score: 11-13 percent depending on the simulation.
Percent of Teachers Rated Ineffective, by Number of Students Opting Out Per Classroom
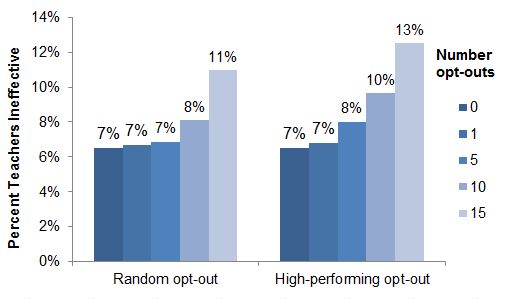
A large number of opt-outs in a classroom also increases the teacher’s chance of getting a high score, as shown in the simulated ratings using the New York scoring system in the figure below.[3] However, in New York, the punishments for a low score are more significant than the reward for a high score. New teachers must now receive good scores in three out of their first four years in order to be eligible for tenure, and teachers with tenure can now be terminated after two years of low scores.
Distribution of Teacher Ratings, with and without 15 opt-outs
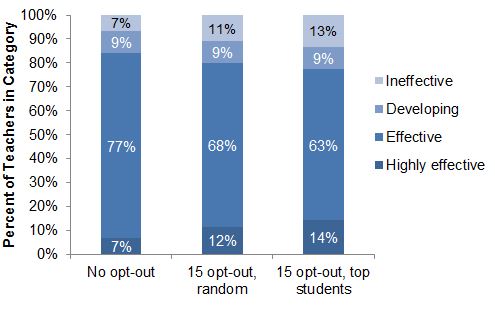
Reducing the number of students who contribute to a teacher’s value-added score not only changes the chance that a teacher will receive a particular rating; it also increases the likelihood that she will receive the wrong rating. One way to assess the potential impact on the fairness of the resulting teacher ratings is to calculate the correlation between teachers’ value-added scores with and without opt-out. If only one student in the class opts out, value-added scores barely change at all—the correlation is 0.99 (on a scale from 0 to 1). With five and ten opt-outs per class, the correlation remains high—0.97 and 0.91, respectively. The correlation eventually starts to break down if a large number of students opt out—it is 0.77 if 15 students do so—indicating a measurably less fair evaluation system than if all students take the standardized tests.[4]
Governor Cuomo has sharply criticized the evaluation system as “baloney” for classifying 99 percent of teachers as effective. The strange irony is that teachers who convince many of their students to opt-out are likely to help achieve Cuomo’s goal of increasing the share of teachers judged to be low-performing. These teachers would also receive evaluation scores that are less fair than the ones produced without opt-out in a system their union already believes is unfair.
But in the majority of classrooms, where opt-out appears likely to remain at low levels, the data strongly suggest that students sitting out of standardized testing will have only a trivial impact on the ratings received by their teachers. The broader lessons is that while opt-out may have some success as a political strategy, it is unlikely to have much of a direct, broad-based impact on the teacher evaluation system in New York or any other state.
Note: After publication of this post, it was brought to my attention that New York State does not report growth ratings for teachers with fewer than 16 students with test scores. The impact that opt-out in conjunction with this rule has on teacher evaluations in New York in the future will depend on whether the rule remains part of the newly revised evaluation system and on the specifications of the performance measures used for teachers without growth ratings. To the extent that these measures are more lenient than growth ratings (i.e. the non-growth measures are less likely to produce a low score than the growth ratings), then opt-out could produce higher ratings for some teachers who have enough opt-outs to push them below the reporting threshold.
[1] Specifically, we analyzed data on the math achievement of fourth- and fifth-grade students in 2009-10 who were in classrooms of 16-30 students. Our value-added measure of teacher performance was estimated as the average residuals from a regression of math scores on prior scores in both math and reading (including squared and cubed terms) and indicators of free/reduced-price lunch eligibility, limited English proficiency status, and disabilities. This model is conceptually similar to but much less complicated than New York State’s model.
[2] This analysis assumes that opt-out is relatively localized, so that while it affects an individual teacher’s estimate it does not affect the statewide distribution against which the teacher is being compared. If opt-out occurred uniformly across the state, then it would have no impact on the share of teachers classified as low-performing because it would shift the distribution for the entire state. Of course it would still increase the mismeasurement of teacher performance, just not the percent in a given category (e.g., more than 1.5 standard deviations below the mean).
[3] The simulation makes an important simplification by using only the teacher’s estimated value-added score and not the confidence range of that estimate (see details on page 6 of this document). This simplification was made for computational reasons; incorporating the confidence intervals into the analysis would likely weaken the simulated impact of opt-out on the share of teachers rated in the highest and lowest categories (because more opt-outs would increase the size of the confidence intervals).
[4] These correlations are from the simulation in which students randomly opt-out. The correlations for the simulation in which higher-performing students opt-out are 1.00, 0.97, 0.90, and 0.72 for one, five, 10, and 15 opt-outs, respectively.




