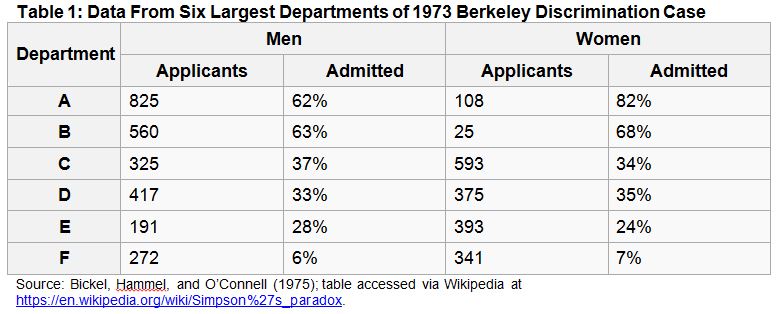
In the early 1970s, the University of California, Berkeley was sued for gender discrimination over admission to graduate school. Of the 8,442 male applicants for the fall of 1973, 44 percent were admitted, but only 35 percent of the 4,351 female applicants were accepted. At first blush, and assuming the applicants’ qualifications were similar, this pattern indeed appeared consistent with gender discrimination. However, when researchers looked more closely within specific departments, this bias against women went away, and even reversed in several cases.
This apparent contradiction, in which the trend of the whole can be different from or the opposite of the trend of the constituent parts, is often called Simpson’s paradox, after British statistician Edward H. Simpson, who described the phenomenon in 1951. In the Berkeley case, the “paradox” occurred because women disproportionately applied to departments with low acceptance rates, as shown in the table above, while men disproportionately applied to departments with high acceptance rates. Examples of Simpson’s paradox have also been found in baseball batting averages, on-time flights of airlines, and even survival rates from the Titanic.
Simpson’s paradox and math results
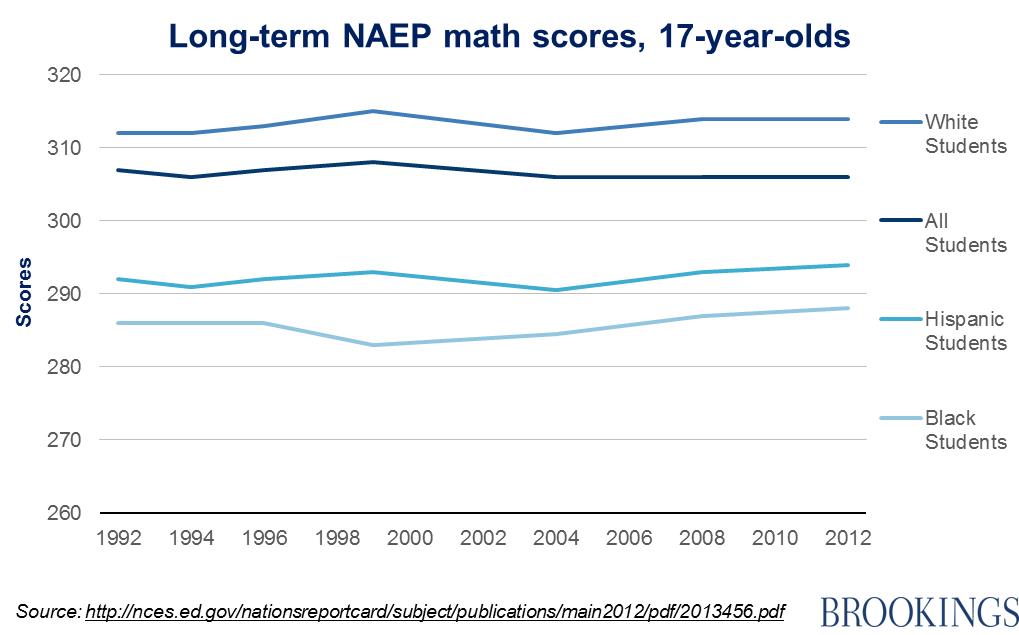
Why might the paradox matter for research or policy? Education is a case in point. According the National Assessment of Educational Progress (NAEP), the only nationally-representative exam measuring student learning over the past few decades, math scores for all 17-year-olds barely budged between 1992 and 2012. In fact, the average score dipped by a point (see the navy blue line below):
But as the graph also shows, average test scores actually rose slightly for white students, black students, and Hispanic students. If each of these groups was performing better, how did the overall average go down? The answer is the composition of students changed. In 1992, 75 percent of students were white, 15 percent were black, and 7 percent was Hispanic. By 2012, 57 percent were white, 13 percent were black, and 22 percent were Hispanic. The modest progress in each ethnic group is not visible in the overall results, since black and Hispanic students have lower average scores.
Simpson’s paradox and median earnings
Another example is the anemic trend in median earnings among prime-age men. Although the lack of growth in earnings for most men is real, the picture is not quite as bad as it first appears. Between the bottom of the early 1980s recession in 1982 up to 2013, inflation-adjusted median earnings of men aged 25 through 44 fell by about $1,000, from $34,000 to $33,000. However, the same earnings measure rose by more than $3,000 for white men, increased just under $1,000 for black men, stayed flat for Hispanic men, and shot up by $10,000 for other men (mostly Asians). Except for those of this last category, these changes are hardly something to crow about, but they’re better than a $1,000 decline.
Once again, the reason for the discrepancy is changing composition of the population: there are now more men in the lower-earning racial categories.
As our society grows more diverse, Simpson’s paradox may make more frequent appearances. Scholars and policy-makers will have to be mindful as they examine long-term changes of social and economic progress. It would be a shame if real progress in these areas was overlooked because of a naïve reliance on single averages.
The Brookings Institution is committed to quality, independence, and impact.
We are supported by a diverse array of funders. In line with our values and policies, each Brookings publication represents the sole views of its author(s).

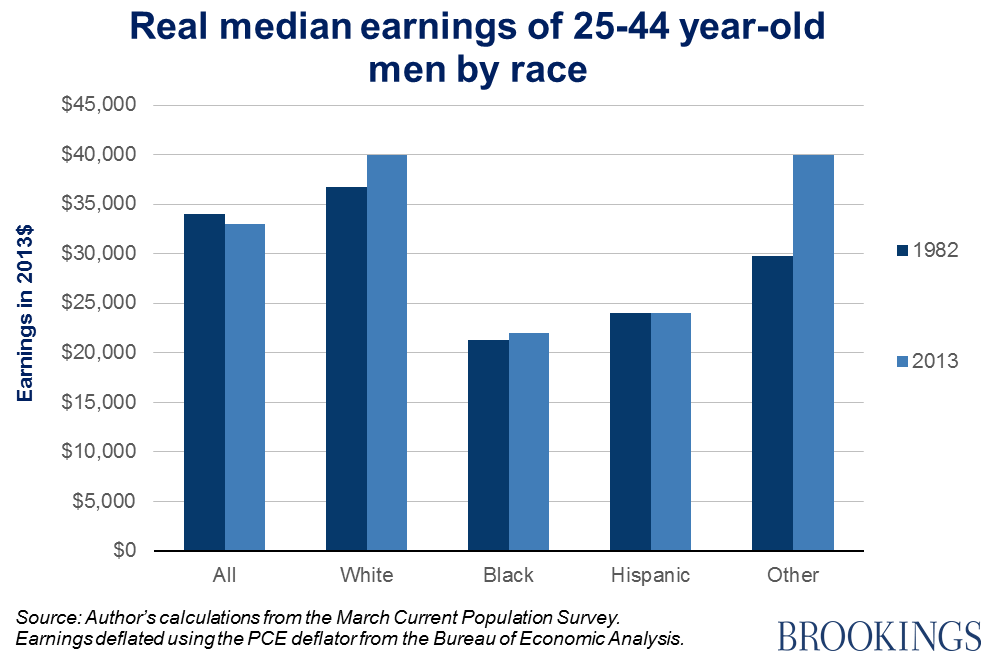


Commentary
When average isn’t good enough: Simpson’s paradox in education and earnings
July 29, 2015