Have you noticed that the testing and accountability movement is in a bit of trouble? A far from exhaustive list of setbacks includes that:
New York City, which for the past 12 years was an epicenter of reform based on the information provided by test scores, is now in the hands of back-to-the-future Bill de Blasio: “I would put the standardized testing machine in reverse. It is poisoning our system.” The new mayor’s overwhelming election success is forcing an uneasy embrace by the pragmatic Clinton wing of the Democratic party, which formerly could be counted on to support testing and accountability – as Bill Clinton did vigorously when he was President. That support is now likely to be muted.
Testing and accountability in Texas took a body blow in 2013 with the legislature passing several bills with overwhelming bipartisan majorities that cut back the number and use of tests. Texas is not just another state on this issue. It was the leader in testing and accountability reforms beginning in the 1990s and the model for the Bush administration’s No Child Left Behind iteration of the federal Elementary and Secondary Education Act (NCLB is still the law of the land 12 years after passage).
Nearly every state in the nation has received waivers from the Obama administration from the accountability requirements of the aforementioned law of the land. These ESEA waivers weaken testing and accountability by allowing, depending on the state, a low cap, e.g., 15%, on the number of schools that are subject to meaningful consequences for low performance; the substitution of vague aspirational goals for the previously required hard time lines and clear criteria for student achievement; and the use of super subgroups for reporting and accountability purposes in place of the specific race-, income-, language-and disability-defined groups that were heretofore the basis for reporting and accountability.
The Common Core State Standards Initiative, fueled by massive infusions of financial support from the Obama administration (through Recovery Act provisions), seemed to be a shoe-in to replace the current mishmash of state standards and tests. But it is now facing a tsunami of opposition from unlikely allies. On the one hand, opposition to the Common Core has become a litmus test for tea-party Republicans, who see the initiative as an open door to further massive federal intrusions into state and local control of K-12 education. On the other hand, we have what Secretary of Education Arne Duncan recently described, in-artfully, as the “white suburban mom” factor. These are parents with children in public schools in up-scale neighborhoods to which they moved precisely because they thought there were buying a good school along with their expensive house. They’re fine with testing and accountability for poor kids in bad neighborhoods but don’t want federal or state officials dictating to the schools that serve their surely-way-above-average little darlings. They’ve pushed back since states began to embrace standards and accountability in the 1990s, but all they succeeded in doing until recently was slowing things down. However, the new Common Core tests are setting the bar for student proficiency at a higher level, which makes a lot of suburban schools and students look bad. In New York State, for example, 31 percent of students reached the proficient level in the first administration in 2013 of the new Common Core tests, down from a 77 percent passing rate in 2009 under the previous, less demanding state tests.
Some of the impacts on student outcomes of the changes these events portend can only be evaluated through lenses that are coloured by assumptions and extrapolations. For example, some observers look at the undeniable advances in student achievement and high school graduation rates that occurred during the era of high stakes accountability and conclude that a rollback of testing and accountability will surely result in lowered results for students. Others look at the same data and conclude that American students would have shown even more progress had their teachers and schools not been hobbled by teaching to the test.
Let’s drill down to a level at which fewer assumptions are involved. In particular, the issue we wish to explore is the impact of reducing the frequency of student testing on the quality of information on school and teacher performance that test results provide. While there are many voices advocating the scale back of standardized testing, it is useful to evaluate something specific. The authors of one such proposal include Linda Darling-Hammond, the Senior Research Advisor to one of the two state consortia developing the new Common Core tests. That is reason enough to single it out for attention:
Congress should require that states ensure external testing for a single grade at each of three school levels—elementary, middle, and high school—while continuing to report scores separately for vulnerable groups.
[i]
Currently the ESEA requires that elementary and middle school students be tested in every grade beginning in grade 3. What would happen to the quality of information that would result if these assessments were cut back to one grade?
First, as is probably intended by Darling-Hammond given her position on teacher evaluation,[ii] the ability to evaluate teachers based on test score value-added would vanish. This is because value-added calculations at the teacher level depend on the difference between the test scores of a teacher’s students at the end of the school year and the test scores of those same students at the end of the previous school year. The annual gain in test scores of the teacher’s students, with some additional statistical information, is the teacher’s value-added. Teachers whose students show greater gains have added more value to their students’ achievement than teachers whose students show lesser gains.
Value-added can’t be calculated for many teachers as it is,[iii] but in the tested grades and subjects in which it can be estimated, it provides an important point of validation for other more widely deployed measures such as classroom observations.[iv] It is also the basis for calculating the school’s value-added, e.g., the test score gains between 3rd and 5th grade for all the students attending a particular elementary school relative to the gains in other elementary schools. But with only one test at each of three school levels, gains can’t be calculated for teachers or schools. The result is that value-added and the useful information it provides is out the door.
Second, and perhaps not part of the implicit motive for the “test-once” proposal, the reliability of information about school performance is weakened, particularly for the “vulnerable groups” about which Darling-Hammond and her co-authors want scores to continue to be reported . What would happen to estimates of student achievement at the school level if we switched from testing three grades to only testing one grade (e.g. from testing in grades 3-5 to only testing in grade 4)?
We examine this question with data from the 2009, 2010, and 2011 school years in 62 elementary schools in a large urban school district with which we are conducting collaborative research. We find that the estimates of school performance become less reliable when using test scores from only one grade instead of three. The hit on the reliability of year-to-year estimates in school performance is only moderate when considering estimates for all students in the school but becomes unacceptably large when reporting for separate subgroups.
These findings are illustrated in the following figure by plots of the variance accounted for in school-level estimates of student achievement from one year to the next (e.g., 2009 to 2010) for all students vs. Hispanic students using data for grades 3-5 vs. only grade 4.[v] The question is: how much of the spread of school-level achievement test scores in a particular year can be predicted from the scores of those same schools in the previous year? We don’t expect schools to remain at the same place in the distribution of test scores from one year to the next because some schools get better and some don’t. But there is a lot of evidence, including that presented in the figure below, that the year-to-year performance of schools relative to other schools within the same district is relatively stable. If we have a measure of school performance that bounces around a lot from one year to the next over a large number of schools, that measure is likely sending a very noisy, unreliable signal of actual school performance.
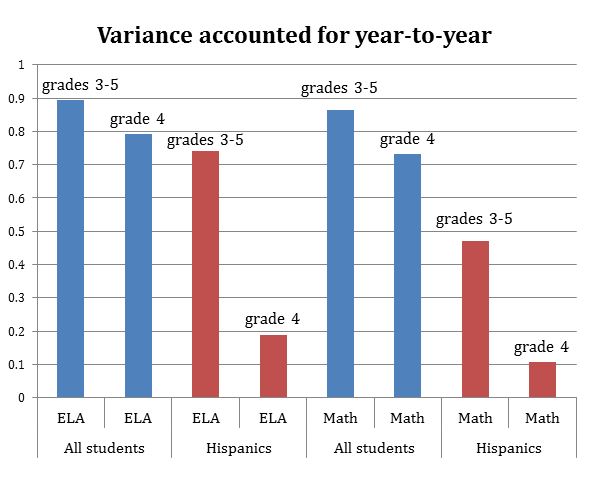
The figure above shows clearly that once we start using only a single grade to calculate the performance of a school for subgroups of students, the drop off in the reliability of the estimates of school performance is so large as to make such estimates practically meaningless. For instance, only about 10% of the differences among schools in a given year in the math performance of Hispanic students can be predicted from the school-level scores of 4th grade Hispanics from the previous year. In contrast, over 45% of the differences among schools in the performance of Hispanic students from one year to the next can be accounted for when the results from testing in three grades are used.
In many schools there simply aren’t enough members of individual “vulnerable subgroups” in the tested grades and subjects to provide an estimate of school performance with respect to those groups that is sufficiently reliable to serve as a basis for school accountability and intervention. This is the well known minimum “n” size issue that bedevilled the measurement of adequate yearly progress under the provisions of NCLB.[vi] We see in the figure the effects of really small “n” size when only one grade is used to evaluate the performance of a school with subgroups – in many cases there aren’t enough students being tested to generate stable estimates.
Whatever the arguments for less testing, reducing the frequency of testing along the lines of the proposal by Darling-Hammond and her co-authors would eliminate the possibility of evaluating individual teachers or schools with metrics that include gains in student achievement. And it would create such high levels of unreliability in the estimates of school level performance for vulnerable subgroups as to undermine any attempt to ensure that these students receive the quality education that they have been historically denied.
Surely if the nation is going to go to the trouble and expense of testing students to see how they and their schools are performing, we want the signal sent by those test scores to be as reliable and actionable as possible. It is psychometrically straightforward that test reliability is strongly correlated with the amount of information that is sampled. Thus, we knew before we conducted our empirical exercise that using one grade to estimate the performance of elementary schools would produce less reliable information than using three grades – the question was only how much. It follows that if we want the most reliable signal from test score data, we should test more not less. Any psychometrician worth his or her salt will tell you this.
Paradoxically, it may also be the case that many of the unintended negative consequences of high stakes student testing would be reduced if we tested more not less. Consider what would happen to the pervasive test-prep sessions that consume weeks of class time in many schools leading up to the end-of-the-year test if students, instead, spent an hour or so monthly being tested on content drawn from their lessons in the previous few weeks. Under this scenario the high stakes tests blend into the tests and quizzes that good teachers have always given their students regularly, and that research shows without a doubt increase student learning.[vii]
Yes, you heard it here: The solution to too much testing is even more testing.
[i] http://www.edweek.org/ew/articles/2013/10/09/07tucker.h33.html?tkn=ZURFviA0ovX3eGaLBrbdhVaQJ1187hIjLQez&print=1
[ii] http://edpolicy.stanford.edu/sites/default/files/publications/creating-comprehensive-system-evaluating-and-supporting-effective-teaching.pdf
[iii] https://www.brookings.edu/blogs/brown-center-chalkboard/posts/2013/04/24-merit-pay-whitehurst
[iv] https://www.brookings.edu/research/reports/2010/11/17-evaluating-teachers
[v] Variance accounted for is the mean of the square of the correlation coefficient between the school level scores from 2009 to 2010 and from 2010 to 2011.
[vi] http://www.ecs.org/clearinghouse/71/71/7171.pdf
[vii] http://ies.ed.gov/ncee/wwc/pdf/practice_guides/20072004.pdf#page=16
The Brookings Institution is committed to quality, independence, and impact.
We are supported by a diverse array of funders. In line with our values and policies, each Brookings publication represents the sole views of its author(s).





