Most of our blogs focus on how to promote social mobility, with a strong bias towards the relative intergenerational kind. But this is an area where the choice of metrics really, really matter. Different measures of relative mobility illuminate different dimensions of the state of opportunity in America.
So, in today’s blog, we examine two measures of intergenerational income persistence: intergenerational elasticity and rank-rank slopes. In a second piece later this week, we will explore measures of movement, specifically conditional transition probabilities and rank directional mobility.
Intergenerational elasticity
The intergenerational elasticity coefficient, often abbreviated as IGE, is the godfather of mobility measures. Used for the last half century, it measures the relationship between the logged family income of parents and the logged family income of their child. A lower IGE coefficient indicates that parental income matters less in terms their child’s income as an adult. In the United States, estimates of the IGE coefficient hover around 0.4 or higher (i.e., if two families have incomes that differ by 10 percent, their children’s income will differ by about 4 percent).
Rank-rank mobility
The rank-rank slope measure measures the association between parents’ rank in the earnings distribution and their children’s rank in earnings distribution as adults. As with the IGE, a lower coefficient indicates more mobility. Recent estimates from Chetty, Hendren, Kline and Saez find that the rank-rank slope in the US is about 0.34, meaning that a 10 percentile increase in parents’ rank in the income distribution is associated with a 3.4 percentile increase in the child’s placement as an adult.
IGE versus rank-rank slope: Pros and cons
IGE is very well-established and allows for comparability of findings to past studies or across countries — which is one reason for its popularity. But IGE estimates are highly sensitive to sampling and to specification (e.g., using lifetime income rather than income averaged over a specific age range). By contrast, rank-rank slope is more robust to specification and sample and allows you to account for people with no earnings (who are dropped when calculating IGE).
Moreover, IGE is far from a pure measure of relative mobility, since it can be strongly influenced by changes in income inequality — unlike rank-rank slopes. Scott Winship from the Manhattan Institute has pinpointed this problem using illustrative scenarios in a recent blog post for e21. We have stolen Winship’s hypothetical examples, and added hypothetical dollar amounts.
Imagine there are equal numbers of two types of workers: Type 1, making between $90,000 and $110,000 a year and Type 2, making between $25,000 and $45,000. In an immobile world, in which parent type wholly determines child type — and earnings for the types remain constant across generations — you would see the following mobility levels using the two measures:
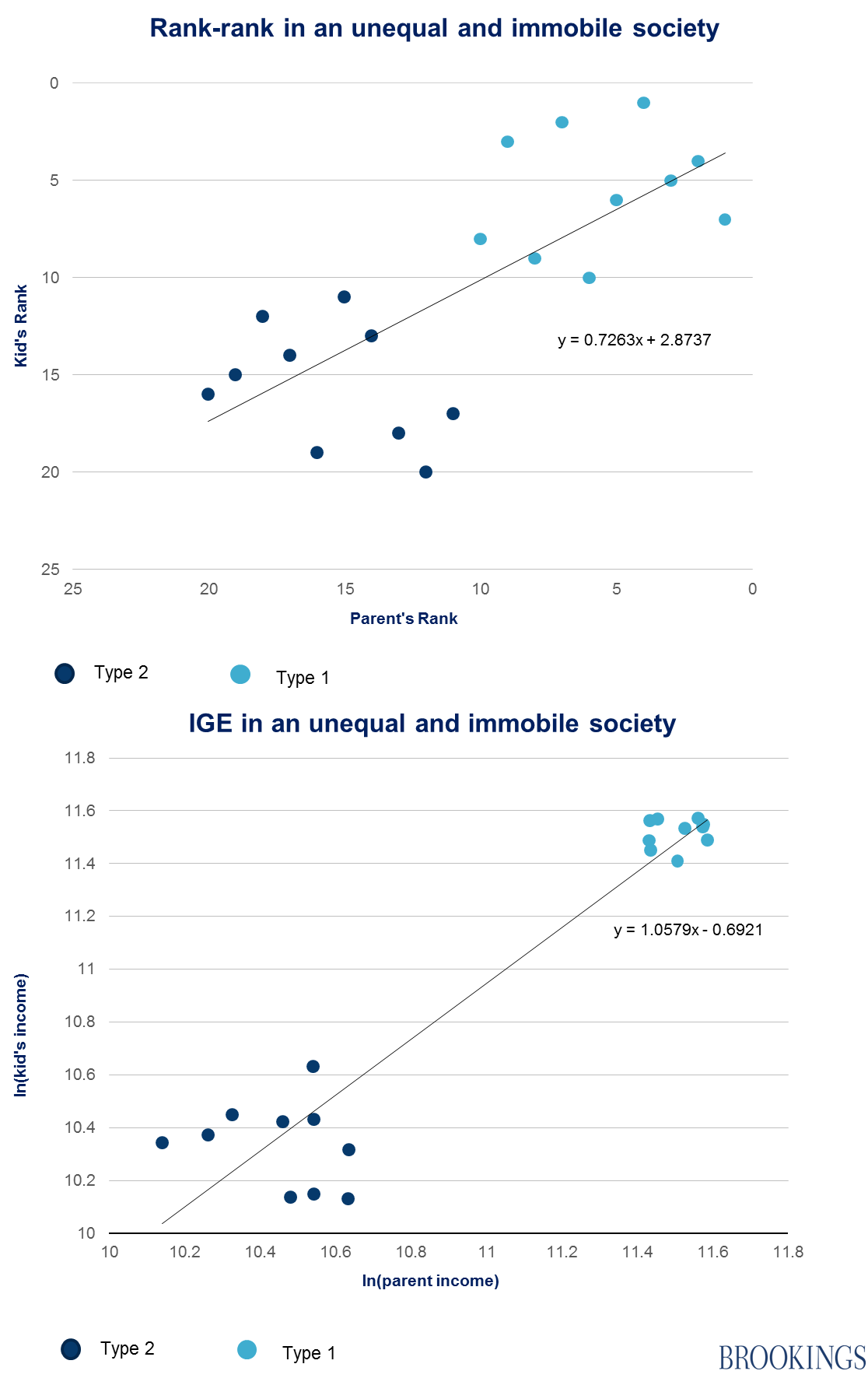
While there’s some movement in rank within the two types, no Type 1 ends up ranked lower than a Type 2. Income of one’s parent almost perfectly predicts one’s income as an adult.
Scenario 1: An equalizing, but immobile world
Imagine that some policy changes — say, raising the minimum wage raising taxes on high income — result in a narrower income gap between the two types in the second generation. Second-generation Type 1s make between $80,000 and $100,000, while Type 2s make between $45,000 and $65,000. But persistence remains absolute: all children are the same type as their parents:
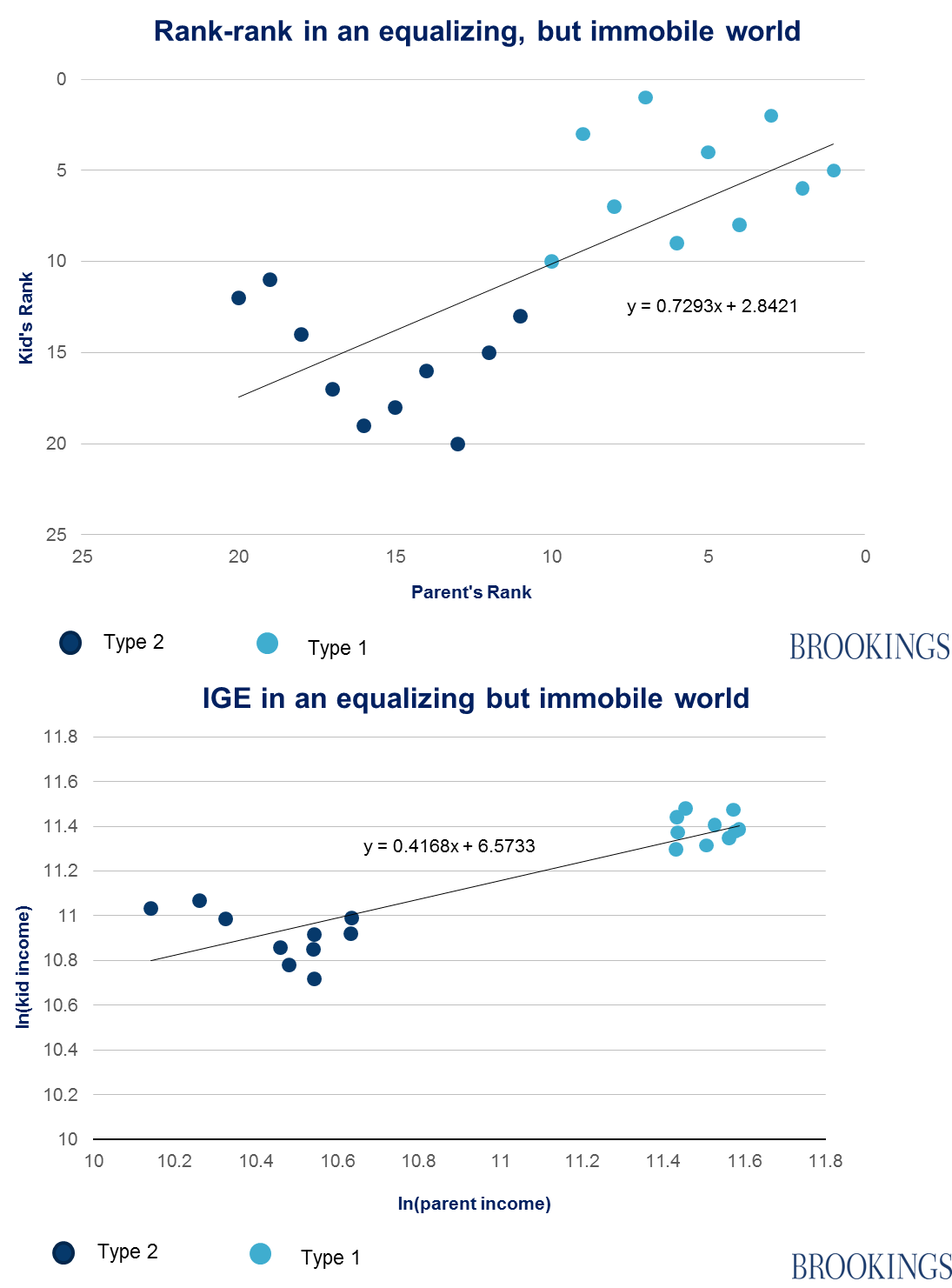
The rank-rank slope is almost identical as in the first society — type one children always remain ranked above type two children— but, as you can see, the IGE coefficient has improved significantly.
Scenario 2: An unequal, but mobile world
In the second scenario, the incomes of Type 1s and Type 2s remain unchanged, but intergenerational ‘type’ persistence is lower: now there is only a 60% chance that a member of the second generation will be of the same type as their parents.
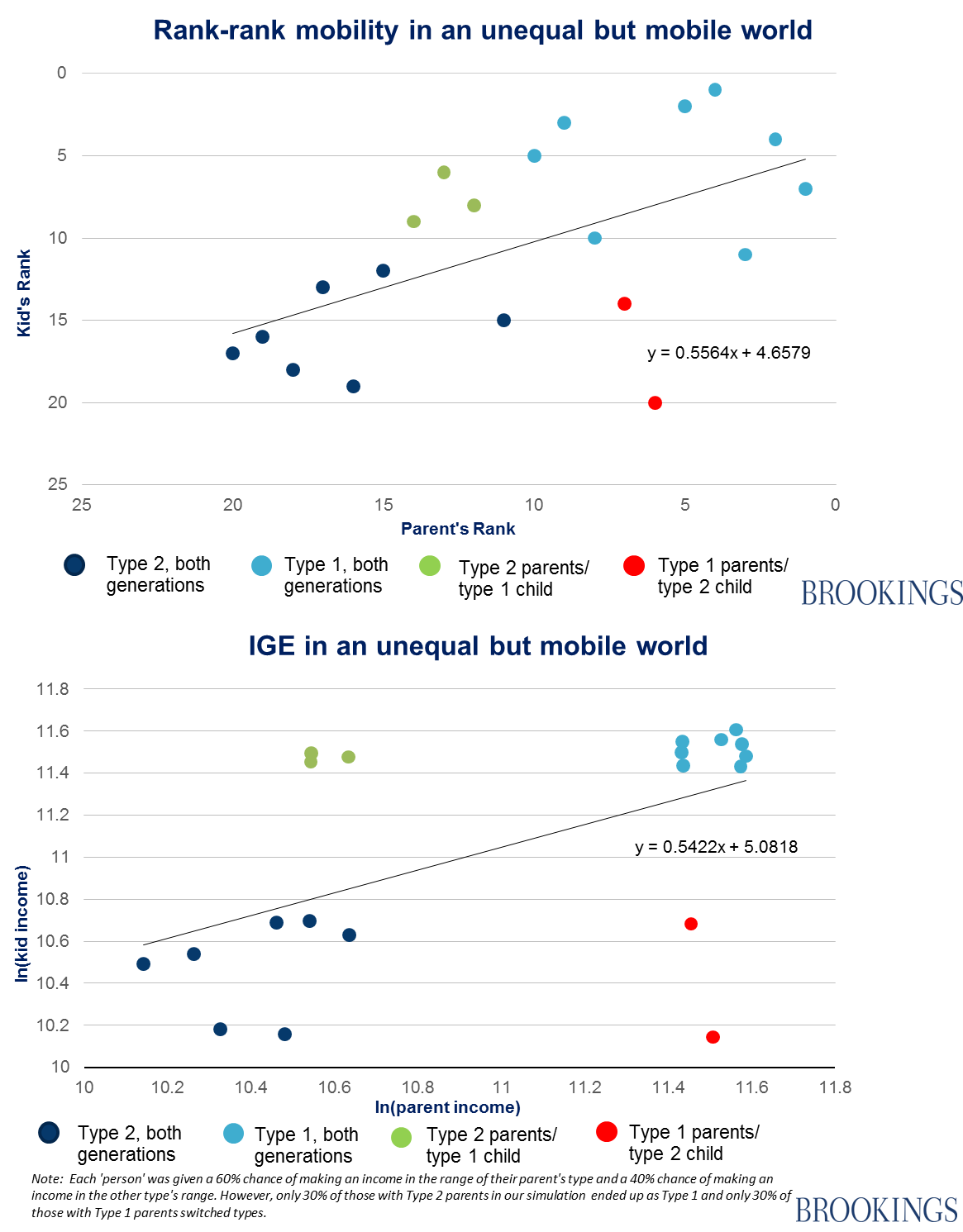
Under this scenario, the IGE measure is worse than in scenario 1, while the rank-rank slope measure is better. Here are the coefficients for the two measures in our ‘starting’ society and under the two change scenarios described:
|
Table 1. IGE and rank-rank slope, for three types of societies |
|||
|
|
‘Starting’ Scenario: Unequal and Immobile |
Scenario 1: Equalizing, but Immobile |
Scenario 2: Unequal but Mobile |
|
IGE |
1.06 |
0.42 |
0.54 |
|
Rank-rank |
0.73 |
0.73 |
0.56 |
The IGE measure picks up a lot of information about the distribution of income at different points in time, as well as movement along the income distribution. The rank-rank slope measure is impervious to income inequality, focusing only on relative position.
This is not to say that either is a ‘better’ measure than the other; simply that the value of any measure depends on the question you are trying to answer.
Intergenerational elasticity
Intergenerational elasticity
The Brookings Institution is committed to quality, independence, and impact.
We are supported by a diverse array of funders. In line with our values and policies, each Brookings publication represents the sole views of its author(s).




Commentary
Measuring relative mobility, part 1
April 27, 2015